Getting Started¶
This page assumes that you have already installed the
pypfilt package, and shows how to generate forecasts for the following
system:
Parameters¶
Particle filter parameters are provided by default_params().
Observation model parameters (and fixed parameters for the process model, if any) should be added to this parameter dictionary, so that all parameters pertaining to the simulation are stored together.
def get_params():
"""The default simulation parameters."""
# The particle filter parameters.
params = pypfilt.default_params(Model, px_count=1000)
# Provide an observation model.
params['log_llhd_fn'] = log_llhd
# System model parameters.
params['sys'] = {'noise_alpha': 5e-3, 'noise_dx': 0.025}
# Observation model parameters.
params['obs'] = {'sdev': 0.05}
# Set a fixed PRNG seed.
params['resample']['prng_seed'] = 42
return params
Observations¶
Observations are represented as dictionaries that have the following keys:
{'date': datetime.datetime(...), # When the observation was made
'value': 200, # The numerical quantity that was measured
'unit': 'Some measure', # A description of the measurement units
'period': 7, # The observation period, in days
'source': 'Some system', # A description of the data source
}
An observation stream is represented as a chronologically sorted list of
observations (oldest first).
The particle filter accepts any number of observation streams, which must be
provided as a list (i.e., a list of observation lists); see
forecast() and run().
Observations can be read from external files:
def obs_from_file(filename, year):
"""
Read observations from a file with the following format:
year date value
2009 2009-01-02 0.680762021741
2009 2009-01-03 0.62923826359
2009 2009-01-04 0.621926239641
2009 2009-01-05 0.618802422847
...
"""
col_types = [('year', np.int32), ('date', '|O4'), ('value', np.float32)]
col_convs = {1: lambda s: datetime.datetime.strptime(s, '%Y-%m-%d')}
df = np.loadtxt(filename, skiprows=1, dtype=col_types,
converters=col_convs)
df = df[df['year'] == year]
nrows = df.shape[0]
# Note that counts are assumed to be reported daily (period = 1).
return [{'date': df['date'][i],
'value': df['value'][i],
'unit': 'x',
'period': 1,
'source': 'file: {}'.format(filename)}
for i in range(nrows)]
They can also be generated synthetically:
def generate_obs(x0, alpha, sdev, start, days, seed=42):
"""Generate noisy observations from a known truth."""
rng = np.random.RandomState(seed)
time = np.array(range(1, days + 1))
# Here, x(t) = x(0) * e^{- alpha * t} + error
xs = x0 * np.exp(- alpha * time)
if sdev > 0:
xs += rng.normal(scale=sdev, size=days)
return [{'date': start + datetime.timedelta(days=i + 1),
'value': xs[i], 'unit': 'x', 'period': 1,
'source': 'synthetic'}
for i in range(days)]
System models¶
The model of the underlying system must inherit from
pypfilt.model.Base.
Here is a simulation model for the example system:
class Model(pypfilt.model.Base):
"""
A model of the following system:
dx/dt = - alpha
The state vector is ``[x(t), alpha]``.
"""
@staticmethod
def state_size():
"""Return the length of a single state vector."""
return 2
@staticmethod
def priors():
"""Return a dictionary of model parameter priors."""
return {
'alpha': lambda r, size=None: r.uniform(0.01, 0.10, size=size),
}
@staticmethod
def init(params, vec):
"""Initialise any number of state vectors."""
rnd = params['resample']['rnd']
rnd_size = vec[..., 0].shape
# Assume that x(0) is somewhere between 0.5 and 1.
vec[..., 0] = rnd.uniform(0.5, 1.0, size=rnd_size)
# Select alpha according to the prior.
vec[..., 1] = params['prior']['alpha'](rnd, size=rnd_size)
@staticmethod
def update(params, step_date, dt, is_fs, prev, curr):
"""Perform a single time-step for any number of state vectors."""
rnd = params['resample']['rnd']
rnd_size = curr[..., 0].shape
# Calculate the deterministic change for x.
dx = prev[..., 0] * prev[..., 1] * dt
# Add stochastic noise to the rate.
noise = params['sys']['noise_dx']
noise *= rnd.normal(size=rnd_size) * dt
dx += noise * np.sqrt(dx / dt)
# Add stochastic noise to alpha.
noise_alpha = params['sys']['noise_alpha']
noise_alpha *= rnd.normal(size=rnd_size) * dt
# Update the state vectors, ensuring alpha remains strictly positive.
curr[..., 0] = prev[..., 0] - dx
curr[..., 1] = np.clip(prev[..., 1] + noise_alpha, 0.01, 0.1)
@classmethod
def state_info(cls):
"""Describe each state variable."""
return [("x", 0)]
@classmethod
def param_info(cls):
"""Describe each model parameter."""
return [("alpha", 1)]
@classmethod
def stat_info(cls):
"""Describe each statistic that can be calculated by this model."""
return []
Observation models¶
The observation model must be stored in params['log_llhd_fn'] and have the
following form:
def log_llhd(params, obs_list, curr, prev_dict):
"""
Calculate the log-likelihood of obtaining specific observations from each
particle.
"""
log_llhd = np.zeros(curr.shape[:-1])
# The expected observation is x(t).
exp = curr[..., 0]
# The standard deviation of the observation error.
sdev = params['obs']['sdev']
# The likelihood distribution for each particle.
obs_dist = scipy.stats.norm(loc=exp, scale=sdev)
for o in obs_list:
# Calculate the likelihood of this observation for each particle.
log_llhd += obs_dist.logpdf(o['value'])
return log_llhd
While the argument prev_dict was not used in this example, it can be used
to obtain the state vectors at the beginning of an observation period:
def log_llhd(params, obs_list, curr, prev_dict):
# Obtain the state vectors for one week prior.
# This is only valid if an observation has a period of 7.
one_week_ago = prev_dict[7]
dx = curr[..., 0] - one_week_ago[..., 0]
...
This is useful for situations where the observation depends on the change in the state vector over the observation period.
Summary objects¶
Simulations typically comprise a large number of both particles and time steps, and so it is generally preferable to record statistics that summarise the particles than to store the entire state history of each simulation.
This functionality is provided by pypfilt.summary.HDF5, which allows
any number of summary tables to be recorded. Once all of the estimation and
forecasting simulations have been performed,
save_forecasts() will save the results to disk.
Here is an example of how to record fixed-probability central credible
intervals for the state variable \(x\) and model parameter \(\alpha\)
of the example system, using the ModelCIs summary
table:
def main(args=None):
"""Generate forecasts against noisy synthetic data."""
params = get_params()
# Define the simulation period.
year = 2009
days = 42
start = datetime.datetime(year, 1, 1)
until = start + datetime.timedelta(days=days)
# Generate noisy (synthetic) observations.
true_x0 = 0.7
true_alpha = 0.05
sdev = 0.03
obs_list = generate_obs(true_x0, true_alpha, sdev, start, days)
streams = [obs_list]
# Define the summary tables to be saved to disk.
summary = pypfilt.summary.HDF5(params, obs_list)
summary.add_tables(pypfilt.summary.ModelCIs(probs=[0, 50, 95]))
# Define the forecasting dates.
fs = [datetime.datetime(year, 1, 2), datetime.datetime(year, 1, 3),
datetime.datetime(year, 1, 5), datetime.datetime(year, 1, 9),
datetime.datetime(year, 1, 16), datetime.datetime(year, 1, 23)]
# Run the model estimation and forecasting simulations.
data_file = os.path.join(os.path.dirname(__file__), 'example.hdf5')
pypfilt.forecast(params, start, until, streams, fs, summary, data_file)
return 0
Forecasting¶
Model estimations and subsequent forecasts are generated by
pypfilt.forecast(), as illustrated in the example above.
This function takes the following arguments:
- A parameter dictionary;
- The start and end of the simulation period (
datetime.dateinstances); - Any number of observation streams;
- The dates at which forecasts should be generated (a
datetime.datelist); - A summary object to calculate relevant statistics; and
- The output file, if desired, otherwise set to
None.
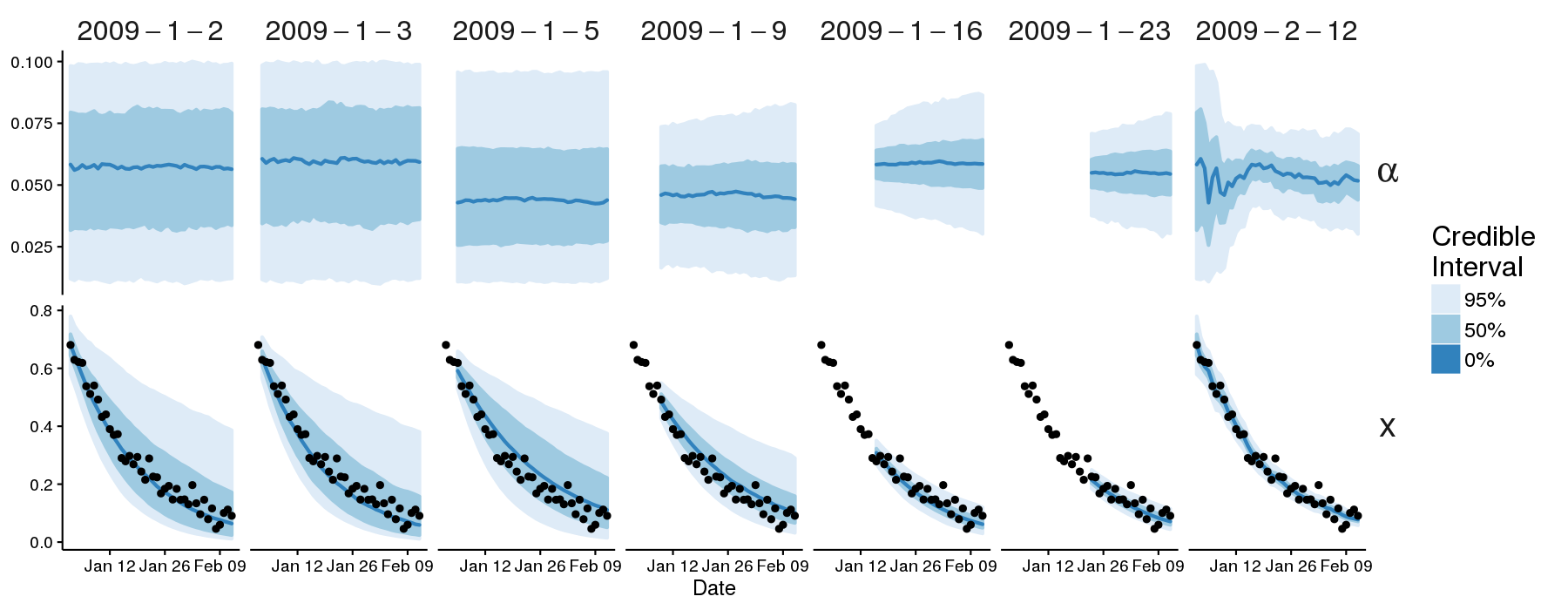
Forecast plots¶
The code presented here is available in the doc/example directory.
To generate and plot forecasts for this system, run the following commands
from the root directory of the pypfilt repository:
./doc/example/run.py
./doc/example/plot.R
This will generate forecasts (stored in example.hdf5) and plot the
credible intervals for \(x(t)\) and \(\alpha\).
Important: the plotting script requires a working version of
R and the following packages:
ggplot2,
rhdf5,
and scales.